[最も好ましい] 正四角錐 高さ 求め方 中1 251284-正四角錐 高さ 求め方 中1

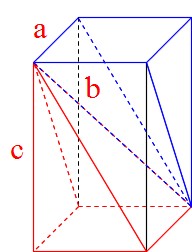
(1) 体積を求めよ。 (2) 表面積を求めよ。 図は底面が一辺6cmの正方形の正四角錐で高さは8cmである。体積を求めよ。 8cm 6cm 6cm 図は底面が正三角形の三角柱である。 A B C D E F (1) 辺ABとねじれの位置にある辺をすべて書きなさい。 (2) 面ABCと平行な面を書きなさい。一般に，1辺が a の正四面体の体積を V とすると， だから， となる． 以上の説明だけではにわかに信じられないという人のために，通常のまともな計算で確かめておこう． 1辺が a の正三角形の高さは， である． したがって，この正三角形の面積 S は，図1．正四角錐の作り方 (2) 正四面体 この正四角錐には底がない。しかし、正四面体にすると、底ができる。 作り方（図2）：正四角錐の側面で、厚さが最も薄い側面に折り目を付ける（左図）。内側に折 り込んで、のりを付けて三角錐にする。のりしろの

正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学

正四角錐 高さ 求め方 中1

正四角錐 高さ 求め方 中1-下の図によって三角錐の体積の求め方を考えます。 上の図のように縦横高さが等しい立方体を半分に切った三角柱を考えると、 この三角柱は、上図のように、体積が等しい（底面積が等しく高さが元の立方体の辺の長さの）3つの三角錐に切り分けることができます。 それで、三角錐の体積は'* @paramin e 正四角錐の斜辺の長さを指定します。 '* @return Variant 正四角錐の高さを返します。 '* @note 関数名の由来：RSQUPYRAMID HeiGhT Public Function RSQUPYRAMIDHGT(ByVal a As Variant, ByVal e As Variant) As Variant RSQUPYRAMIDHGT = (4 * e ^ 2 2 * a ^ 2) ^ 05 * 05 End Function '* @fn Public Function

つぎの正四角錐の側面積 高さ 体積を求めてください 三平方の定理です Clear

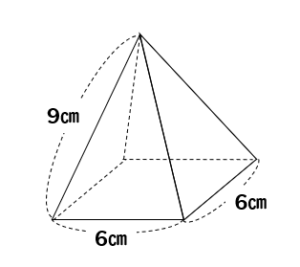
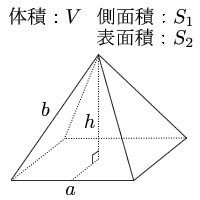
V=h (S1S2√（S1×S2))/3, V：体積, h：高さ, S1：下底面積, S2：上底面積この公式で算出した数値と、少数以下が多少違いますが参考にどちらが正しいでしょうか例えば 上部から数センチ下がり時の容積を簡単に計算出来ないでしょうか？ keisanより 四角錐台の体積は、オベリスク形状を含めた広義で扱っており（上底と下底の長方形が非相似を含む）、体積V=h/6* (AbBa2 (abS q u a r e p y r a m i d (1) h e i g h t h = √ 4 l 2 − 2 a 2 2 (2) v o l u m e V = 1 3 a 2 h (3) s u r f a c e a r e a S = a 2 a √ a 2 4 h 2 S q u a r e p y r a m i d (1) h e i g h t h = 4 l 2 − 2 a 2 2 (2) v o l u m e V = 1 3 a 2 h (3) s u r f a c e a r e a S = a 2 a a 2 4 h 2体積＝6 2 ×π×3√5÷3＝36√5π（ ） 円すいの体積の公式 底面積×高さ×1/3 正四角錐の体積 底辺の1辺が6cm 他の辺が9cmの四角すいの体積を考える 三角錐 四角錐 円錐 三角柱 四角柱 円柱の底面積と体積の求め方を教えてください。 このカテゴリの回答受付中の

台形の高さ・面積（4辺の長さから） 台形の1辺・面積（3辺の長さと高さから） 台形の1辺・面積（3辺の長さと高さから） ひし形の面積 ひし形の面積 平行四辺形の面積 （底辺と高さから） 平行四辺形の面積（底辺と高さから） 平行四辺形の面積底辺の長さと高さを入力し「正四角錐の体積・表面積を計算」ボタンをクリックすると、正四角錐の体積・表面積・斜辺の長さを計算して表示します。 底辺の長さ a： 高さ h： 底辺の1辺の長さaが2、高さhが3の正四角錐の体積・表面積・斜辺の長さ 体積 V：4 側面積 S 1 ： 表面積 S 2正四角錐の高さの求め方について底面が18cm四方の正方形側面の二等辺三 台形の体積 って何 相似の考え方を利用して四角錐台の体積を求め 錐体の表面積6 宿題解説 正四角錐の体積 表面積の求め方 Youtube 四角錐台 体積 中3 数学右の図3は正四角錐の投影図ですこの四角錐の 立面図は1これが四

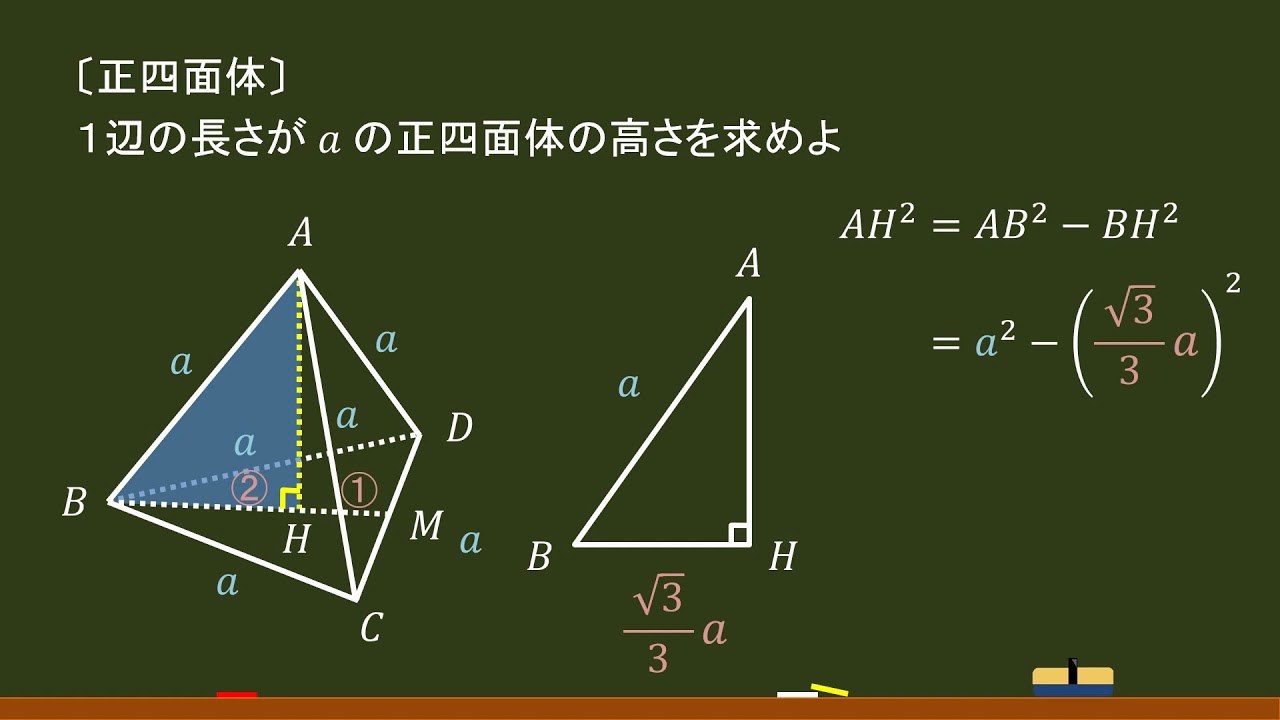
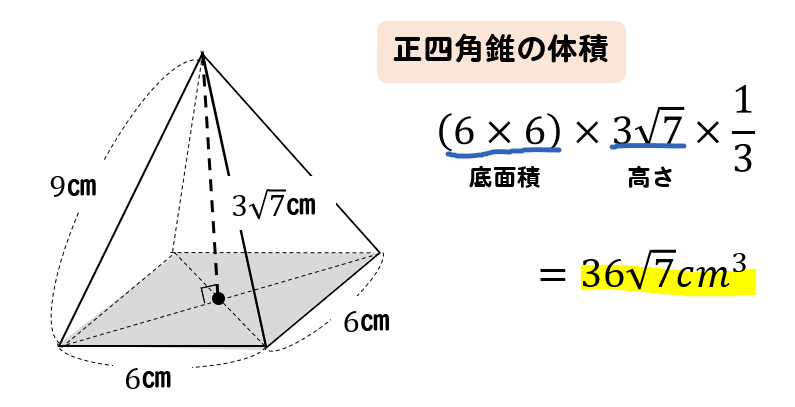
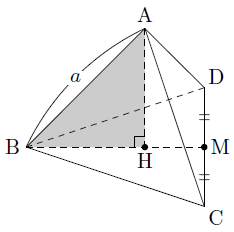
この正三角錐の高さ \(OH\) は下図のようになっています。 \(AM\) を \(21\) に分ける位置に点 \(H\) があります。 \(AM\) は\(1\) 辺が \(2\sqrt{3}cm\) の正三角形の高さで、 \(3cm\) です。 \(OH\) が何\(cm\) なのか求めます。 当然、三角形 \(OAH\) に三平方の定理を用います。3 次の立体の表面積と体積を求めなさい。 (1) 正四角錐 (2) 円錐 5㎝ 9 ㎝ 6 ㎝ 7㎝ 三平方の定理⑥ 空間 図形への利用（1） B 学 年 3 年 学習日： 月 日（ ） 中学校数学・ワークブック 中学校数学 3 －6B 年 組 氏名 解答 年 〔 Point 〕 ① 図形を取り出し、平面図をかく。 ② 1辺がaで③ 錐体の体積＝底面積×高さ× 1 3 ① ②より，この正四角錐の体積は， 18×3

子供向けぬりえ 最新正四角錐 高さ 求め方

正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学

中学数学 高さしかわからない四角錐の体積の求め方 高さが6cmの正四角錐で側面がすべて正三角形です。 その体積の求め方を教えてください。 ちなみに答えは144㎤です。 導き出し方教えてください！高さ・・・h として代入すると 18 3 = 9 7 × h ÷ 3 h = 6 7 21 2 図の正四角錐は底面が1辺12cmの正方形で それ以外の各辺はすべて10cmである。 辺ACの中点をM,辺ADの中点をNとし、辺BC,辺ED上 にそれぞれPC=QD=3cmとなる点P,Qをとる。 面MPQNで正四角錐を2つに切断したとき正四角錐台の体積の求め方の公式 を紹介するよ。 よかったら参考にしてみて。 台形の体積（正四角錐台）の求め方の公式！？ 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。

四角錐の表面積の求め方 公式 小学生 中学生の勉強

台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ

正四角錐 底辺と高さ 体積 表面積の計算 計算サイト 錐体の表面積1 例1正四角錐の表面積の求め方 Youtube 表面積の求め方 計算公式一覧 優れた 四 角錐 の 表面積 壁紙 配布 簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ 正四底面が1辺6cmの正三角形で,上の面にふたのない高さ6cmの三角柱の容器がある。 (1) この容器の中に,すべての側面と底面に接する球を入れる。この球の半径は cmである。また,この状態で容器を水で満たしたとき,その水の量は cm 3で ある。ただし,球は水に1504 ケンサワイ 簡単公式正四角錐の表面積の求め方がわかる3つのステップ 正四角錐の表面積の求め方って？？ こんにちは、この記事をかいているKen

正四面体の公式まとめ 体積 高さ 内接球 外接球 重心 理系ラボ

超簡単 体積の求め方 苦手な数学を簡単に

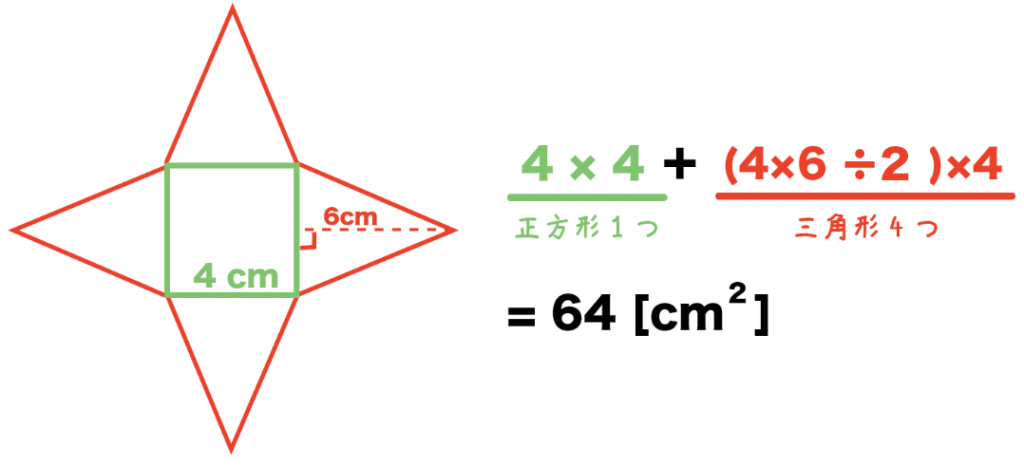
要点四角錐，三角錐，円錐の体積 三角錐，四角錐，円錐の体積 V は，それがちょうど入る四角柱，三角柱，円柱の体積の です． 特に，円錐については，底面の半径が r であるとき，底面積が S=πr 2 と書けるから と書くこともできます． · 正四角錐の高さを求める4ステップ 正四角錐の高さの求め方はつぎの4ステップだ。 補助線を描きいれる。 底面の正方形の対角線の長さ、その半分の長さを出す 高さ（垂線）と底辺をふくむ直角三角形をさがす。 三平方の定理を使って計算する。 つぎの例題をいっしょに解いていこう。 練習問題 つぎの正四角錐の立体の高さを求めなさい。右図のような立体の体積・表面積は，四角錐の高さなどを三平方の定理で求めてから計算します。 右図は底面が1辺の長さ4cmの正方形，側面が1辺の長さ4cmの正三角形です。 体積を求めるには底面積×高さ÷3の公式を使いますが，そのためには高さOHを先に計算しておく必要があります。 (1) OHを

高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ

正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学

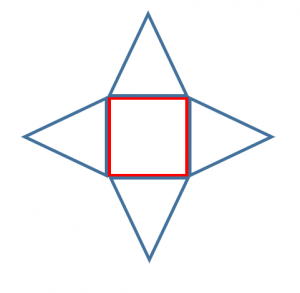
(1) 正四角錐の展開図の一例です。正四角錐なので、底面は正方形、側面は二等辺三角形になるので、その点 に注意して展開図をかきます。 (2) 円錐の展開図の一例です。円錐の展開図における側面はおうぎ形になります。また、展開図の底面は、お$$(体積)=(底面積)\times \color{red}{(高さ)}\times \frac{1}{3}$$ 高さが必要になります。 なので、 まずは正四角錐の高さを求めることから始めましょう。 最初に注目するのは底面の正方形です。正四角錐の体積の求め方を確認する。 数学的活動 〔成り立つ事柄を予想する活動〕 教科書172ページの例題2に取り組み、正四角錐の高さの求め方を考える。

41 Vsqrtcm 1 Lihat Cara Penyelesaian Di Qanda

中3数学 正四角錐の高さの求め方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく

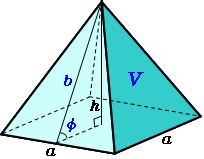
正四角錐の底面が正四角形です。底辺の長さ (a) が等しいです。縦辺の長さ (b) も同等です。側面が二等辺の三角形です。正角錐の高さの基点が底面の中心と一致します (O) 。 角錐の側の面が側面を形成します。正四角錐の場合は、側面が二等辺の三角形です。対角線の長さをxとすると、 x^2乗＝5^2乗＋5^2乗＝50 x＝√50＝5√2 で、写真の図みたいに考えると、 正四角錐の高さをyとして、また三平方の定理を使って、 5^2乗＝y^2乗＋(5√2/2)^2乗25＝y^2乗＋25/2 y＝5√2/2 これで高さが分かったので、あとは質問者さんが考えた通りに正四角錐の体積を求めて、2倍すればいいと思う正四角錐の体積（底辺と高さから） 答えを知れて良かったが、途中式が分からないので、あまり勉強にはならなかった。 a=8,h=3にすると体積がになります。 (14桁の場合) 正しくは、64です。 修正お願いいたします。 失礼致しました。 ご指摘ありがとうございます。 修正致し

計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

Sqrt3 1 6cm 6cm O Lihat Cara Penyelesaian Di Qanda

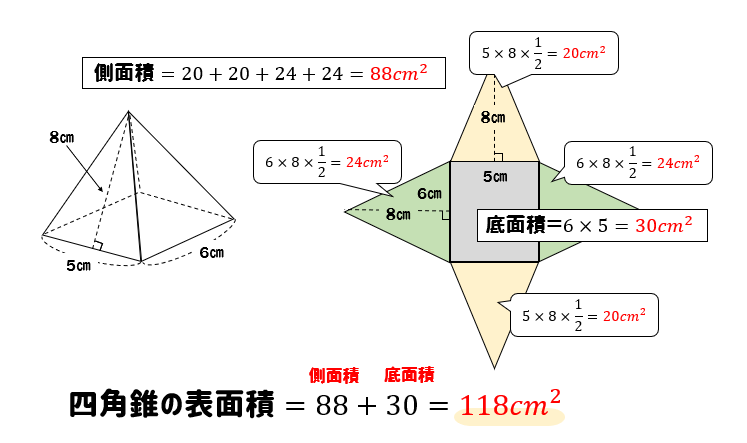
角錐の高さと体積 解説 次の図のようなすべての辺の長さがaの正三角錐（正四面体）abcdについて考えます。 頂点aから底面bcdに垂線ahを引くと，このahの長さが正四面体の高さになります。このとき，図のように abhに着目すると直角三角形であるので，三平方の〇 四角錐の体積は、底面積を求めて高さをかける、そして\(\times \frac{1}{3}\)を忘れないように！ 四角錐の表面積 このように四角錐の展開図は、 四角形の底面、三角形4つ分の側面 になります。「三角錐の重心Oの位置は、その高さの4分の1になります。」 以下に、三角錐の重心の性質の簡単な求め方を示します。 上の図のように、三角錐の重心を3次元座標の原点Oにして考えます。 三角錐ABCDの頂点の座標の平均 （A＋B＋C＋D）／4 が三角錐の重心です。 図のように、A＋B＋C＋D＝（0，0，0）となるように座標を定めます。 ここで、三角錐の底面の三角形BCDの

四角錐の体積の求め方 公式 小学生 中学生の勉強

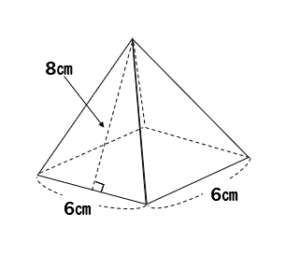
3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ

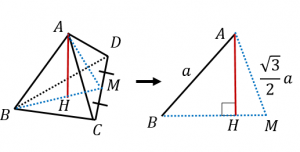
正四角錐の高さは、√2a/2 まではすぐ出るでしょう。 球を正四角錐の1つの側面で切り取ったものは、片面凸レンズのような形になりますが、 その高さは、(3√6)a/6 となります。 高さが分かれば、その体積が出せますね。正四面体の高さの求め方 一辺の長さが の正四面体ABCD (図1)の高さを求めましょう。 頂点Aから正三角形BCDに下ろした垂線の足を点H (図2を参照)とする。 点Hは正三角形BCDの重心になっているので、直線BHと辺CDとの交点を点E (図2を参照)とすると となります。 なぜそうなるかというと、 重心は頂点と対辺の中点を結んだ3本の線の交点 を意味しており、相似を用いて21三角錐でも良いが、すべての面が合同な正三角形なので正四面体が最も適切である。 (2) 正四面体acfhの体積を直接出すことは無理なので、 立方体から、いらない部分を引き算して求める。 いらない部分は全て同じ形の三角錐である。

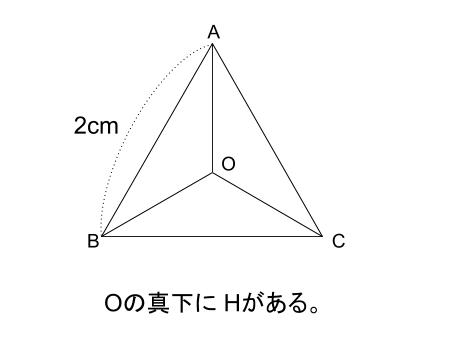
オリジナル 三角錐 高さ 求め方 中学 画像ブログ

正四角錐と三平方の定理 中学３年数学 Youtube

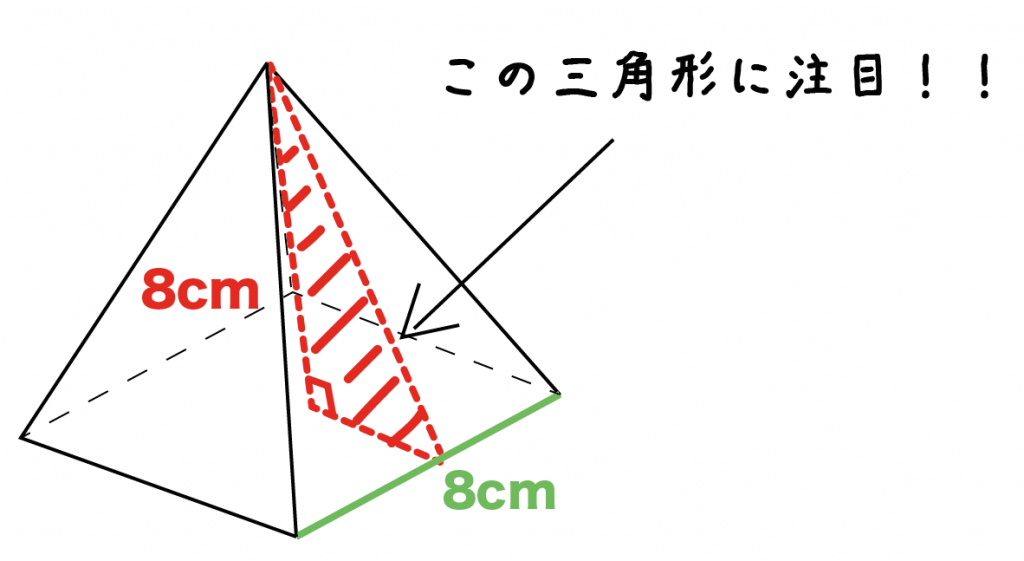
簡単公式正四角錐の表面積の求め方がわかる3つのステップ このとき、 「正四角錐の高さ」と「側面の三角形の高さ」を1辺とする三角形を考えてみよう。 9 なので問題の立体は となっています。 二側台塔回転斜方二十・十二面体• 底面の正方形の1辺の長さをb上の図を見てみよう。 「正四面体」とは、全ての面が 「正三角形」 、つまり、 辺 も、 角度 も、 すべて等しい 特別な四面体だよ。 この「正四面体」は、実はスゴい特徴を持っているんだ。 実は 「『1辺』 の長さが分かれば 『高さ』 も 『体積』 も求められるということ。 なぜそんなことができるのか。 それが今日のポイントだよ。 POINT · 正四角錐って底面が正方形で、先がとんがっている立体のことだったよね。 底面の1辺の長さをa、高さをhとすると、体積はつぎのようにあらわせるよ。 1/3 a²h つまり、 （底辺の1辺）×（底辺の1辺）×（正四角錐の高さ）÷3 ってことだね。

中3数学 正四角錐の高さの求め方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく

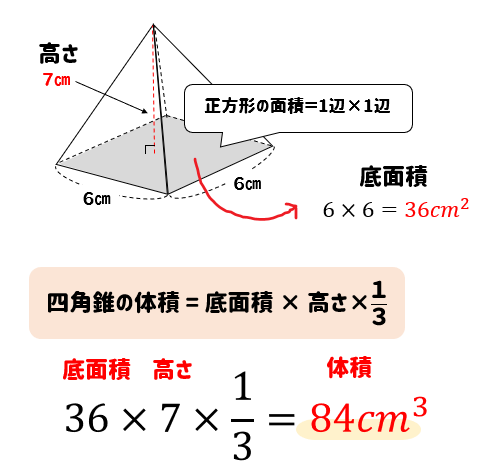
3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ

1辺6の正四面体に内接する球の半径を求めよ。 6 2 1辺16の正方形を底面とする、高さ15の正四角錐に内接する球の半径を中3数学 正四角錐の高さの求め方がわかる4つのステップ Qikeru 高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ 三平方の定理の利用 四角錐 円錐 チーム エン

三平方の定理を利用して四角すい 円すいの体積を求める 無料で使える中学学習プリント

四角錐の表面積の求め方 公式 小学生 中学生の勉強

簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

Mathematics 角錐の体積が角柱の３分の１になる証明 働きアリ

立体の体積 無料で使える中学学習プリント

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

どうして1 3なの 錐の体積の公式の求め方 まなべーと

4 1 8c M 6cm Lihat Cara Penyelesaian Di Qanda

正四角錐の定義 展開図 表面積 体積 具体例で学ぶ数学

正四角錐の体積の求め方や高さの求め方などがわかりません教えてください Yahoo 知恵袋

つぎの正四角錐の側面積 高さ 体積を求めてください 三平方の定理です Clear

錐体の表面積1 例1正四角錐の表面積の求め方 Youtube

四角錐の２点間の距離等の求め方が分かりません 中学数学に関する質問 勉強質問サイト

計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

子供向けぬりえ 元の正四 角錐 の 体積

中1数学 三角柱 四角柱の表面積の求め方がサクッとわかる 映像授業のtry It トライイット

円錐 体積 の 求め 方 三平方の定理 円錐の高さが 体積を求める問題を解説

なぜ 錐体 は3で割る 簡単な説明を 正多面体 から伝授します 横山 明日希 ブルーバックス 講談社 3 4

立方体の中の四角錐の底面積の求め方教えてください Clear

高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ

簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ

四角錐台の体積 高精度計算サイト

錐体の表面積6 宿題解説 正四角錐の体積 表面積の求め方 Youtube

中3数学 正四角錐の高さと体積 5分で学習 Youtube

この写真の正四角錐の高さの求め方教えてください 四角錐の体積の公式 Yahoo 知恵袋

三平方の定理の利用 四角錐 円錐 チーム エン

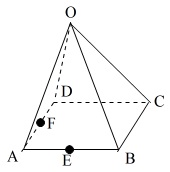
円錐 すい の表面積や四角錐 五角錐の体積の求め方

2 Ab Ab P Lihat Cara Penyelesaian Di Qanda

全ての辺が10センチの正四角錐の高さ 体積 表面積を教えて下さい Clear

84 2 Mefの面積の求め方 中学数学に関する質問 勉強質問サイト

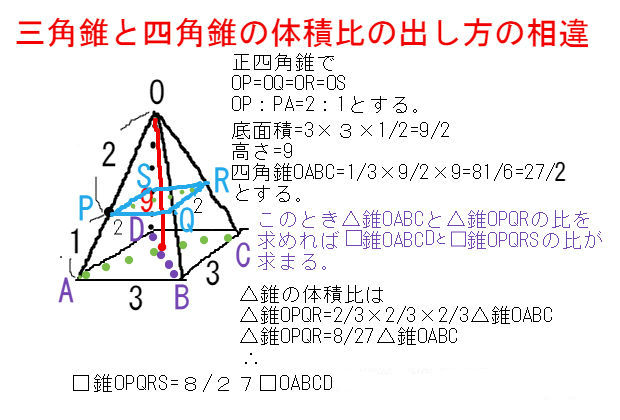
子供向けぬりえ 無料ダウンロード正四 角錐 公式

立体図形 中学数学に関する質問 勉強質問サイト

この写真の正四角錐の高さの求め方教えてください 四角錐の体積の公式 Yahoo 知恵袋

この正四角錐の高さの求め方をおしえてください Clear

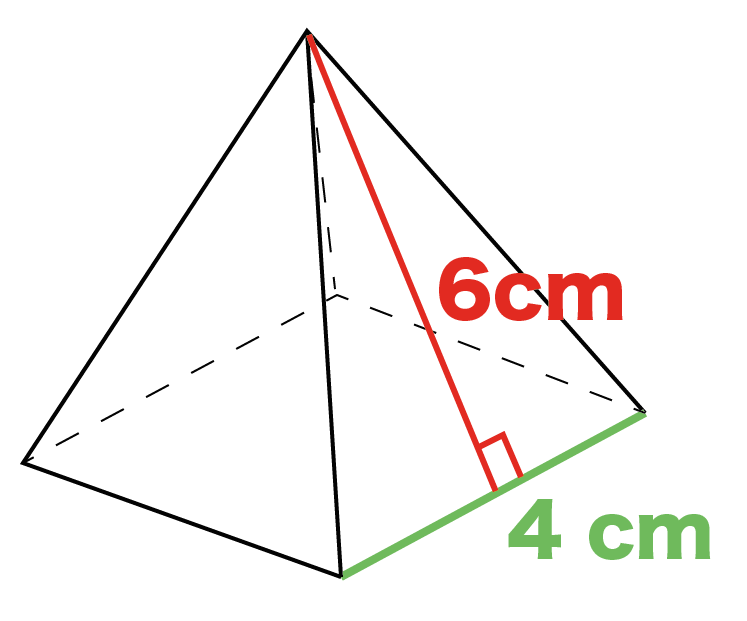
簡単公式 正四角錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

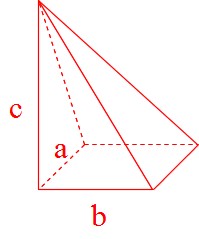
Mathematics 角錐の体積が角柱の３分の１になる証明 働きアリ

正四角錐 底辺と高さ 体積 表面積の計算 計算サイト

中3数学 正四角錐の高さの求め方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく

角錐の高さと体積 まなびの学園

3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ

正四面体の高さと体積の求め方 具体例で学ぶ数学

計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

質問です 中一です 下の図のような一辺10cmで 高さが12cmの正四角 Yahoo 知恵袋

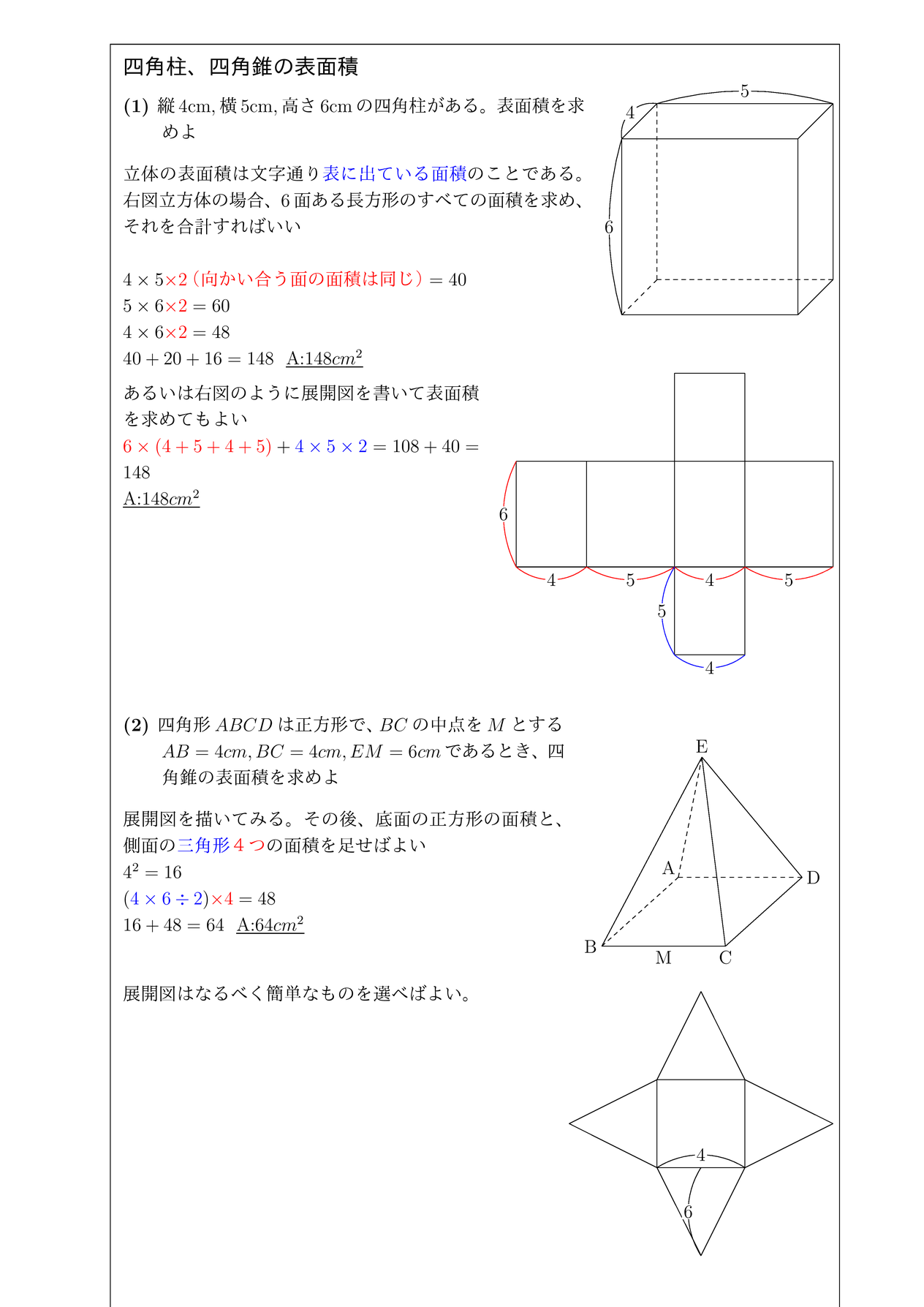
四 角錐 表面積 角錐 円錐の体積と表面積の公式 数学fun

7 1 10c Oabcd Lihat Cara Penyelesaian Di Qanda

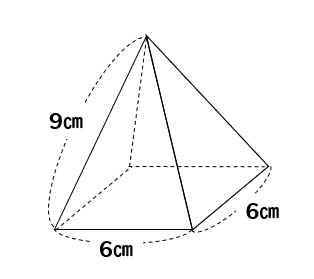
高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ

この体積と表面積の求め方を教えてください Clear

子供向けぬりえ 最新正四角錐 高さ 求め方

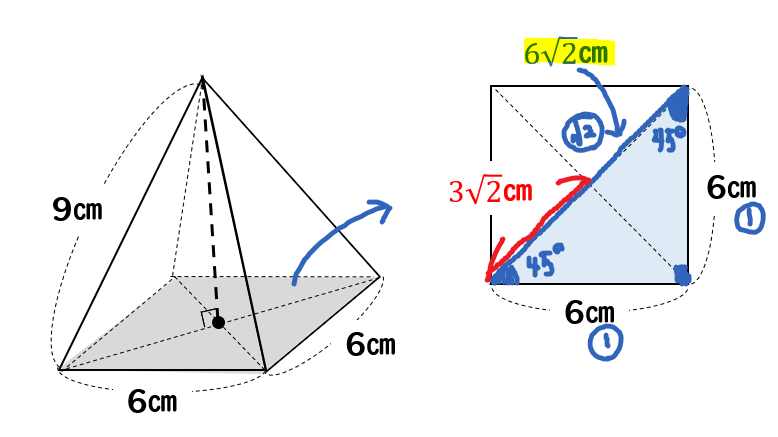
高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ

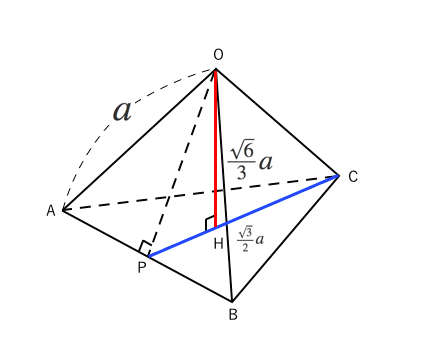
子供向けぬりえ 最新正四角錐 高さ 求め方

中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

正四角錐の体積 底辺と高さから 高精度計算サイト

四角錐の体積の求め方 公式 小学生 中学生の勉強

数学 青チャートa 例題101 正四角錐の高さ 高校数学に関する質問 勉強質問サイト

イメージカタログ トップ 100 正四 角柱 の 体積 の 求め 方

中3数学右の図3は正四角錐の投影図ですこの四角錐の立面図は1辺の長さが6c Yahoo 知恵袋

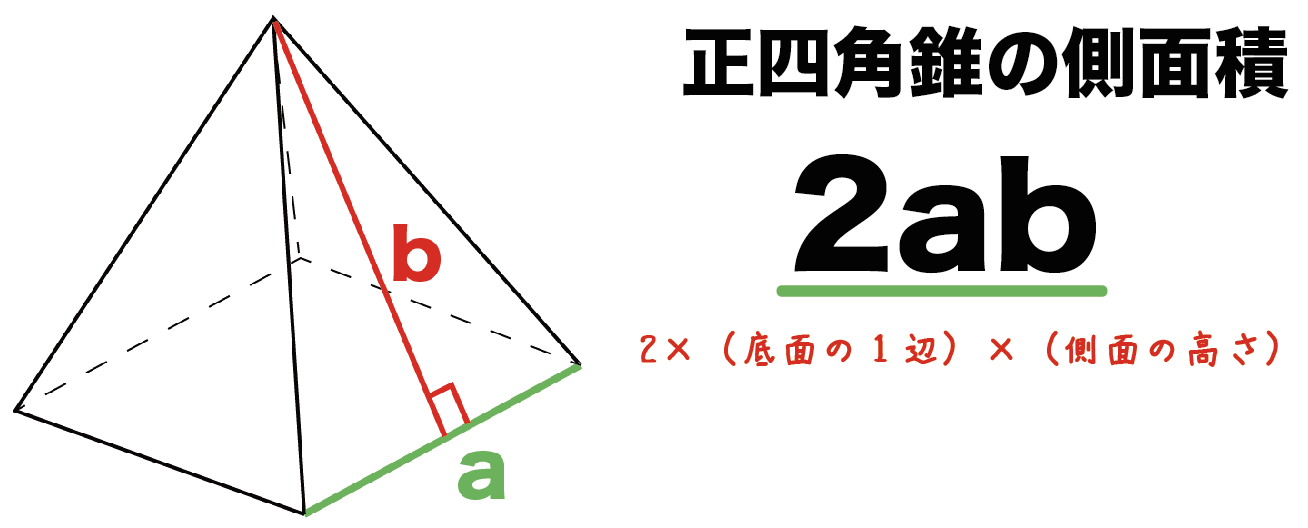
計算公式 正四角錐の側面積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく

中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット

中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

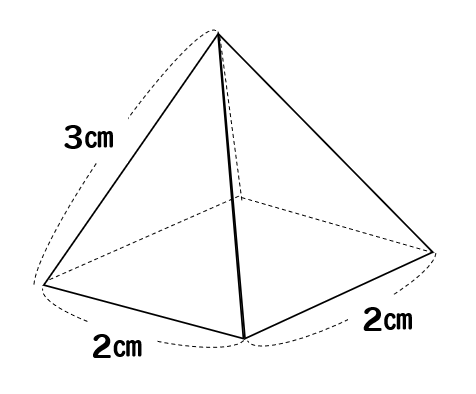
高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ

至急お願いします 中3数学です 正四角錐の投影図から体積を求める問題です Clear

正四角錐の高さの求め方について底面が18cm四方の正方形側面の二等辺三 Yahoo 知恵袋

中２数学 中学数学に関する質問 勉強質問サイト

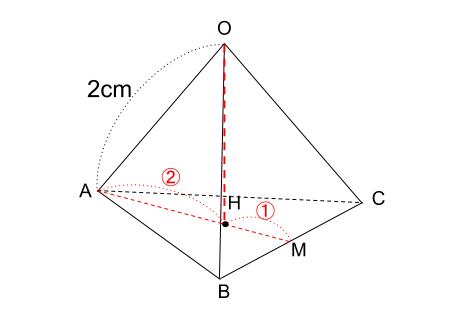
正四面体の体積と三角形の重心 中学数学の無料オンライン学習サイトchu Su

正四角錐についての問題です この Ii の問題の解き方を教え 中学数学に関する質問 勉強質問サイト

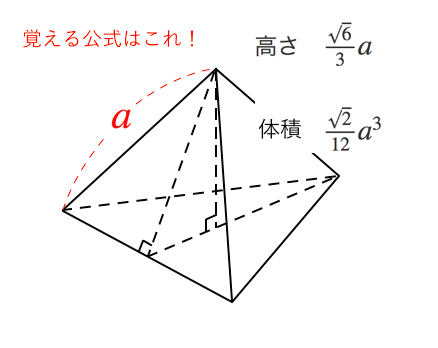
正四面体 高さ 面積を求める公式 苦手な数学を簡単に

計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

角錐 円錐の体積と表面積の公式 数学fun

角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun

円錐や角錐の体積の求め方 中学１年数学 Youtube

円錐 体積 の 求め 方 三平方の定理 円錐の高さが 体積を求める問題を解説

正四角錐の外接球 数学カフェjr

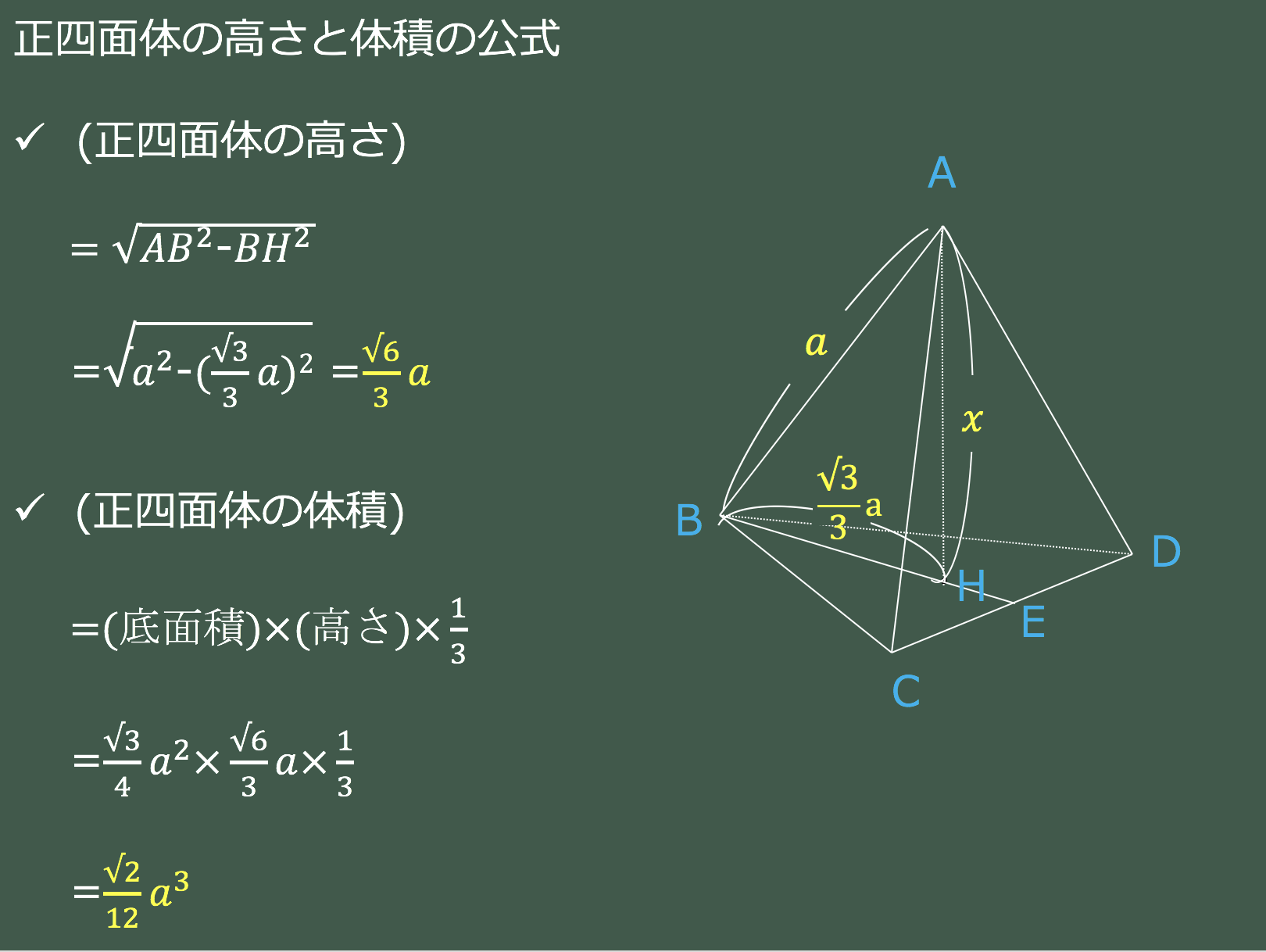
子供向けぬりえ 50 素晴らしい正四角錐 高さ 求め方

台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ

角錐 円錐の体積と表面積の公式 数学fun

四角錐の体積の求め方 公式 小学生 中学生の勉強

灘 正四角錐の切り口の面積 ジーニアス 中学受験専門塾

学習支援 まなびの函 中１ 空間図形 ４ 立体の表面積 ２

体積の求め方 計算公式一覧

Incoming Term: 正四角錐 高さ 求め方 中1,